Wave Function Esoterica

  'Esoteric Encyclopedia of Musical Scales with Polygons and Chord to Time Signature Conversions,  Applied'

by Anthony Vargas

***This was written for major thirds players, astrologers, data scientists, mathematicians and quantum scientists in mind***

Legend

Chord Conversion Process

This process borrowed from the Esoteric practice of Numerology.
In this system all integers(numbers) are added together to form numbers between 1 and 9. The exception being "Master Numbers" such as, 11, 22, 33. These master digits take on their own unique aspects, having the qualities of both their added-up forms and their signature numbers.

To convert a chord into a time signature, sum each interval of your chord, add 1 for every sharp(#) interval and subtract 1 for every flat(b) in your chord. For example:

major triad 

1 + 3 + 5 =
[9]


once you derive this top number (9), round this integer to the nearest subdivision. Typically subdivisions are formed with the integers of: 1, 2, 4, 8, 16, 32, 64, 128, 256, etc.

In the case of this Major triad, 9 is closest to 8, therefore becomes 9 over 8; or 9/8.

In the case of a Minor triad.

Minor triad

1 + b3 +5 =
[9-1] =
[8]

8~8 (8 rounds to 8 in this case), therefore this time signature is 8 over 8; or 8/8.

As you can see, this helps with identifying a particular chord quality to a time signature. Along with that though, is the ability to combine different chord qualities and result in complex/compound time signatures.

If we combined this Major and Minor triad in a loop, it would derive a 17/8 time signature from two simple triads, and in any key!

Further, once you start combining multiple chords, you get a lot of different options. One trick that I've found for combining time signatures is that if you play the even-ordered time signature LAST in the sequence it results in a more natural, smooth rhythm. Conversely, if you play the odd-ordered time signature LAST it results in a more stuttered, asymmetrical rhythm in your cadence. 

This can be utilized for an abrupt or smooth effect really, really well so keep that in mind.

Some numbers result in additional effects, for example a summed integer of 6, which yields an equidistance from a subdivision of 4 and 8. The nature of this allows it to be both and even at the same time for interesting effects.
A summed integer of 1 yields several options as well. Those integers being 1/2, 10/8**, and n/n**.

**Even though 10 is not a Master Number, a larger number CAN still be treated as such and therefore be rounded accordingly to the nearest subdivision.

**N/N is a very special case because 1 as a summed integer, rounded is technically 1 over 1, or 1/1. Anytime a 1 is over itself, it can be treated the same as ANY integer over itself. This serves as a kind of special placeholder function in a time signature cadence for specific use or just to experiment. It should also be noted that while 1/1 is equivalent to n/n, this is not to be confused with other integers that are over themselves, such as the common 2/2, 4/4, 8/8, or 16/16 signatures. Ideally, those are fixed while n/n is mutable or not-fixed.

That being said, if you choose to deviate from this proposed model then that is also highly encouraged as well. Different cadences and augmentations to the value of integers will result in totally different rhythmic and harmonic patterns, which can be better suited for the user's personal preferences!

 

Now onto the scales!
Also for clarifications sake -

A scale is the initial pattern of tonal steps.
A mode is the "retrograde" (backwards movement) of that initial pattern by 1.

For example:

Scale:

(WH)WW

Mode 2:

WW(WH)

Mode 3:

W(WH)W


Notice how the "(WH)" moves backwards from the starting position by 1 placement. The next mode is derived from another backwards movement of 1; and then again.

 In actuality, the entire sequence is fixed and is revolving like a horizontal wheel, or a Planet/celestial body. The objects(intervals) on that wheel eventually revolve back to their starting location, starting the cycle all over again.

If you have an understanding of Einstein's concepts of Relativity, these functions all still apply within the contexts of rhythm and harmony. Music is as much a component of observable and non-observable Physics as it is an art form/medium of expression! How cool is that!?



So lets begin..

Whole Tone Scale

A little commentary with this one. I chose this as the first scale because I find that because each interval of the scale is exactly one whole tone ("W"), that this should be the scale that is taught to all beginners and anyone new to harmonic theory. Much more so than Ionian Major because it introduces something novel to the ears, it's extremely easy to remember and honestly, an understanding of the formation of every other scale is derived from this one especially. If nothing else, once learned this can be modified immediately to find all other patterns. Don't get me wrong, the Ionian Major scale is immensely useful in most Western applications, but it's not intuitive to learn as a beginner in Harmonic functions and with too much emphasis on a Western/Eurocentric pedagogy it winds up serving more as a barrier of entry to the music languages than not. 

Also note how every chord from the first degree or position of the scale (also known as the root position) is identical to all other positions of this scale because of the fact that all of the intervals of the scale are equidistant. The only other Western-Common scale that exists with this quality is the Chromatic Scale, comprised of all (13) Half Steps (H); however the Chromatic Scale utilizes every note within the 12TET (Toned Equal Temperament) System.


W = HH;


WWWWWWW

vs

HHHHHHHHHHHHH

Additionally through these scales you'll see symbols such as (WH) or (HW); in these instances,

(WH) or (HW) = HHH,

(WW) = HHHH,

As you can see, different combinations of even and odd ordered intervals can be combined to create some pretty unique and flavourful combinations!

Minor Pentatonic 

Notice here how the initial scale was the MINOR pentatonic, however by 1 retrograde (mode 2) we've discovered the MAJOR pentatonic, which forms the basis of what we know as the Major Scale!


One thing always leads to another, it seems..

Anyways-

Melodic Minor

This pentagram looking thing shows the same information as the upper chart, it's just a different perspective of the same thing. Wherever there's an "x" is which side of the connecting line that an interval DOES NOT naturally connect with.

For example,

 C or Interval 1 does NOT connect to D or Interval 2
but
D or Interval 2 DOES naturally connect to C or Interval 1.

Despite this information, one can still play either note whenever and however. It's just visual analysis.

Harmonic Minor

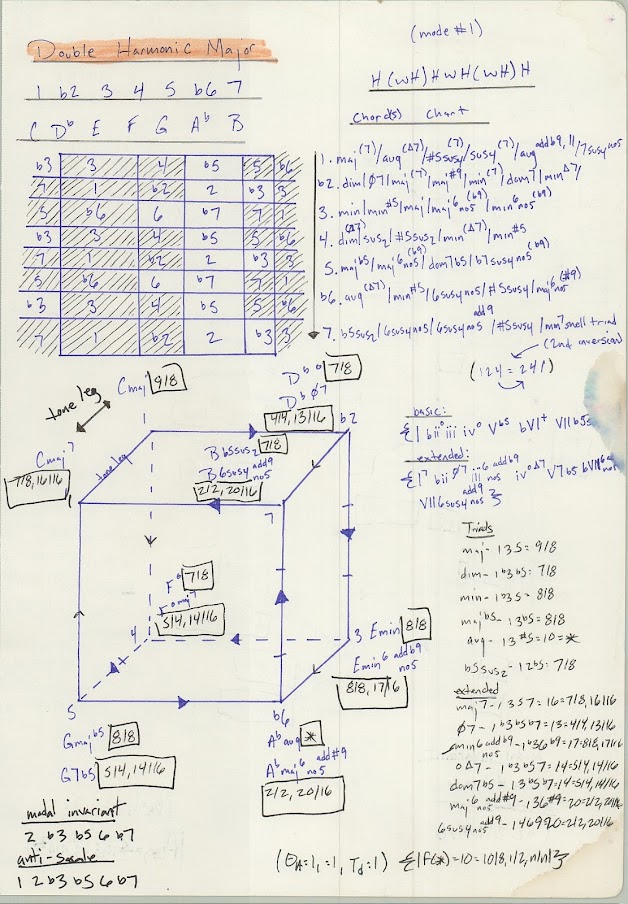
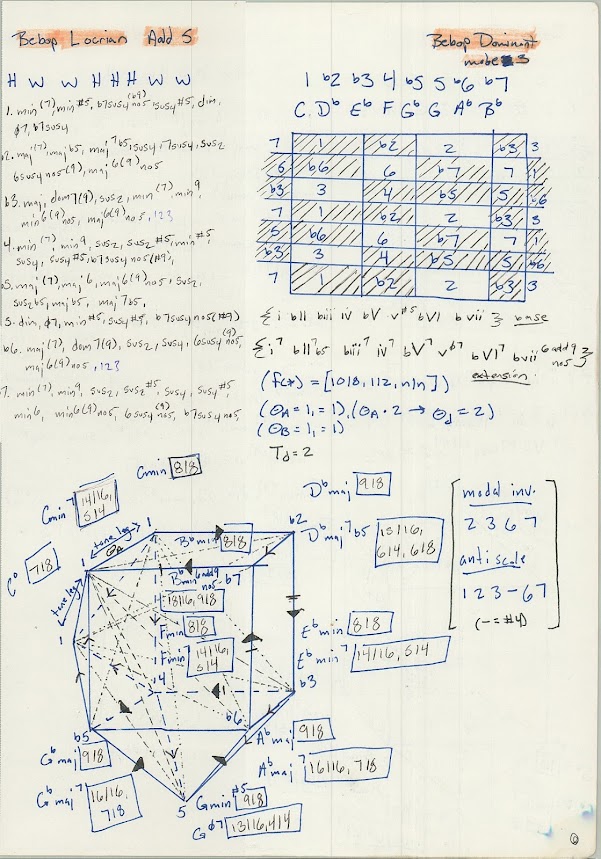
What is a Modal Invariant?

A Modal Invariant is simply any note that is NOT naturally occurring in the scale. 
In this case the modal invariant intervals are : 

2  3 5 b6 and 7

Also known as "Blue Notes" as per the older jazz lexicon or "Spicy Notes" as per modern musical language. Alternatively, "Bad/Awful/Horrible Notes" by many non musicians.

Perspective is one hell of a drug.

What is an Anti Scale?

An Anti Scale is simply any note NOT naturally in the scale but including the root note.
Or in other words, the "1" and all the notes NOT in the scale.

I have heard the argument that the 4th or 5th degree should also be included to match the number of intervals of the original scale, for example:

1 2 3 4 5 6 7

vs

1 b2 b3 4 b5 b6 b7 

or

1 b2 b3 b5 5 b6 b7

While you certainly could do this, I haven't experimented enough with this idea and to keep it simple I just stick with the Root + Modal Invariant notes so that it's clear what's happening.

Moving on...

I got mixed up and placed the(WH) interval in the wrong location for the rest of this set. Again, this is merely a rough draft but I caught the mistake in posting here so that's a fortunate thing. That being said, I am sorry for the informational error.

And now...!!

Ionian Major

Just like the Minor/Major Pentatonic series, but a few more steps!

Ionian b5

Augmented

Diminished

Kumoi

Hirajoshi

Neapolitan Major

Composite II

Locrian Natural 7

Enigmatic Major

 

Enigmatic Minor

This one inspired an idea that I have yet to expound.
Notice the inside of this Tone Cube.

Anyways.. continue

Dominant Sus

Pelog

Persian

Nonatonic (mode 3)

 

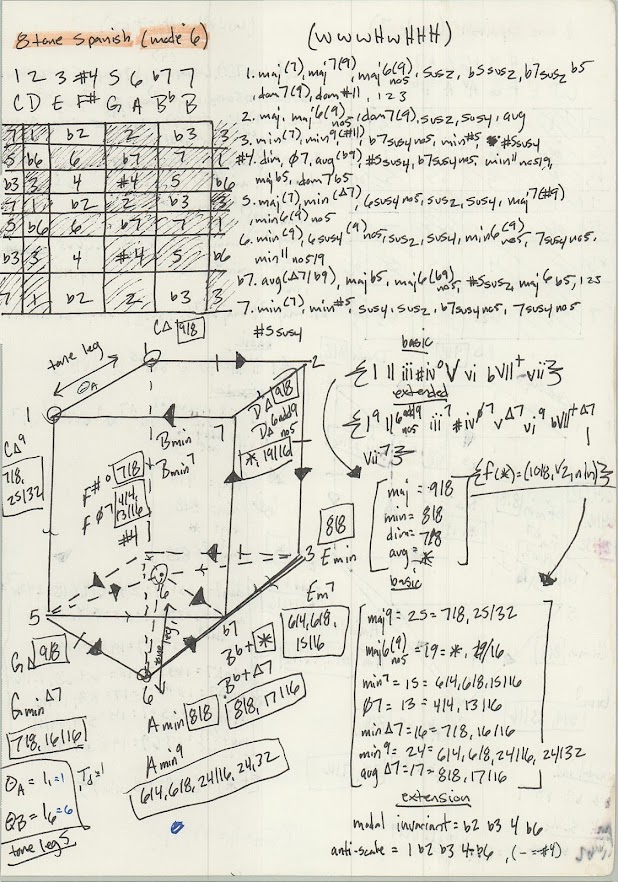
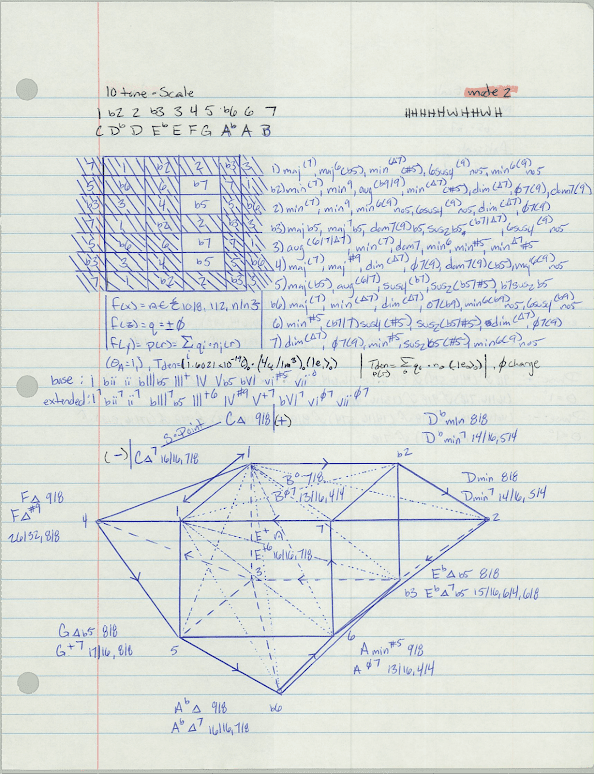
 So, this portion of the notation for the tonal theory book is dedicated to the 8, 9, 10 and 11-tone scales and most of  their respective modes. This includes a breakdown of typical scale permutations, tonal-depth analysis and composition techniques revolving around the geometry of the figures, as well, a slightly deeper analysis of tone legs as an integrated system. 

This concludes the transition from the typical scalar expressions (such as the pentatonic, diatonic, etc.) and resolves to the next installment, which will be mainly focused on the various expressions or rather, cadences of the electron and the integration of harmonic dynamics into the electrostatic purview.

If you haven't read the first installment, I would backtrack there first. Otherwise, enjoy! 

[**To be updated **]

Tone Depth Inquiry

This is asking about the density of the tone leg specifically. That is, if you added more legs of the same interval, how can this be notated, what are some different ways to visualize this concept?

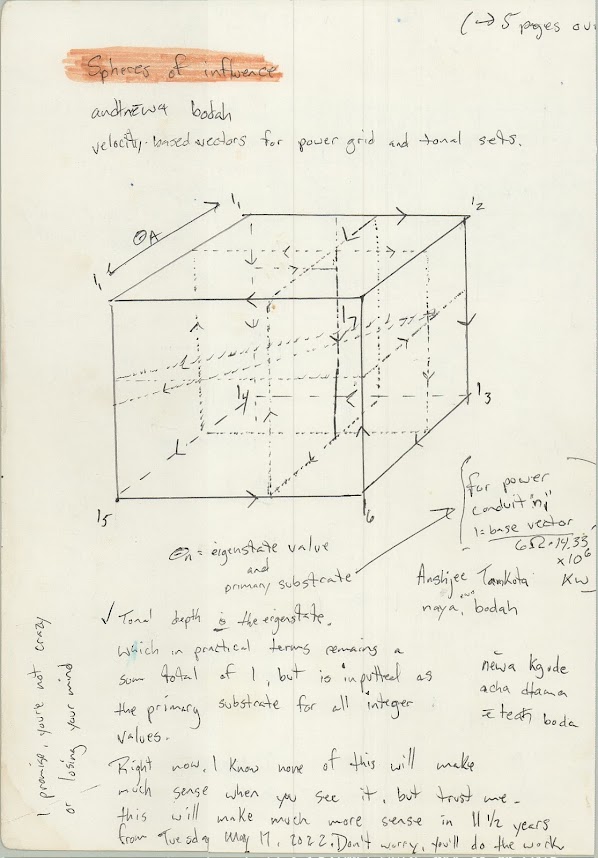
Tonal Velocity and a potential suggestion for

n-microtonal notation, 'n' is the TET subdivision 

 (i.e 12TET, 19TET, 81TET, etc. ).

Once further developed, I think that there can be some serious application for microtonal music.

 

+ Tone Cube and the unit chart of Tonal Orbitals
+  Flashes of Insight; Pleiadean.

Meter Rate Notation and decimal conversion

Ionian b5

+ Prime Scalar,
  Anti-Prime Scalar v Modal-Invariant Scalar formation

[edit: 

anti scale formation - 

(1) 2 3 #4 #5 #6 ,

 modal invariant formation -

( ) 2 3 #4 #5 #6

end:edit ]

Love & Harmony/m^ 3

Flashes of Insight; Pleiadean. (cont.)

+ Tonal Density Cloud

 

+  Entanglement Field Integration

+ Double Harmonic Major mode 5

+ Double Harmonic Major mode 4

+ Double Harmonic Major mode 3

+ Double Harmonic Major mode 2

 +  Double Harmonic Major mode 1

+ Bebop Major mode 8

+ Bebop Major mode 7

 + Bebop Major mode 6

 +  Bebop Major mode 5

 +  Bebop Major mode 4

  + Bebop Major mode 3

 + Bebop Major mode 2

+ Bebop Major mode 1

  + Bebop Locrian Natural mode 1

        Td, or Td(n) - Tonal depth

+ Bebop Locrian Natural mode 6

+ Bebop Locrian Natural mode 5

+ Bebop Locrian Natural mode 7

+ Bebop Locrian Natural mode 8

+ Bebop Locrian Natural mode 4

+ Bebop Locrian Natural mode 3

+ Bebop Locrian Natural mode 2

+ Bebop Dorian mode 7

+ Bebop Dorian mode 6

+ Bebop Dorian mode 5

+ Bebop Dorian mode 4

+ Bebop Dorian mode 3

+ Bebop Dorian mode 2

+ Bebop Dominant mode 8

                        + Bebop Dorian mode 1

+ Bebop Dominant mode 7

+ Bebop Dominant mode 6

+ Bebop Dominant mode 5

+ Bebop Dominant mode 4

+ Bebop Dominant mode 3

+ Bebop Dominant mode 2

+ Bebop Dominant mode 1

+ Scales Utilizing Intervals: b2 and b6


 

+ 9tone mode 1

[one of three of the Messiaen modes, or the 'Limited Modes of Transposition'].

+ 8tone Spanish mode 8

+ 8tone Spanish mode 6

+ 8tone Spanish mode 5

+ 8tone Spanish mode 4

+ 8tone Spanish mode 3

+ 8tone Spanish mode 2

+ 8tone Spanish mode 1

+ 8tone Spanish mode 7

+ 10tone mode 1 + phase oscillation series expansion

+ 10tone mode 2 + phase oscillation series expansion

+ 10tone mode 3 + phase oscillation series expansion

+ 11tone mode 2 tonal density + phase oscillation series expansion

+ 11tone mode 3 + phase oscillation series expansion

+ 10tone mode 4 + phase oscillation series expansion

+ 11tone mode 5 

+ 11tone mode 7 phase oscillation series expansion

+ 11tone mode 8 + phase oscillation series expansion

+ 11tone mode 9 + phase oscillation series expansion

+ 11tone mode 10 + phase oscillation series expansion

+ 11tone mode 11 + phase oscillation series expansion

+ Double Harmonic Major mode 6

Tonal Density Notation 

Table of Mathematical Symbols

pg.1a-c.

Rhythmic Notation & Quantization

Tonal Matrices Layout & Fourier Transform Application

Tone Cube;
 Energy + Thermal Index

A more detailed mapping of a harmonic cubic and some of its constituent nodal properties whilst acknowledging the thermodynamic properties of the surface planes and the volume of vacuum free space or volumetric symmetries and densities.

Thanks,
Stay hydrated.